표본분산을 구할 때 n이 아닌 n-1로 나누는 이유를 3가지 방식을 통해서 알아볼 거에요.
6. Why Dividing by N Underestimates the Variance
6. Why Dividing by N Underestimates the Variance
1) 표본분산을 구할 때 n이 아닌 n-1로 나누는 이유 (자유도)
$S^{2} = \frac{1}{n-1}\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}$
표본분산은 n개의 편차를 사용하는 것같지만 '편차의 합 = 0'이라는 제약조건 때문에 n-1개의 편차 정보를 사용한다.
$\sum_{i = 1}^{n}(x_{i}-\overline{x}) = 0$ : 편차의 합이 0이 되어야 하기 때문에 n-1 개의 편차가 정해지면 n번째 편차는 자동으로 정해진다.
n번째 편차는 단순히 합을 0으로 만들어주는 역할밖에 하지 않기 때문에 사용할 수 없는 정보다.
n-1 : 자유도 (degreee of freedom)
2) 표본분산을 구할 때 n이 아닌 n-1로 나누는 이유 (증명)
$\overline{X}$ 대신에 v를 넣고 그래프를 그린다.

v로 해당 식을 미분한다.

이 값은 v에 대한 곡선의 기울기를 알 수 있다.
v로 미분한 값 = 0인 점이 분산이 가장 작은 곳이다.
5개의 표본을 뽑는다고 하자 $X_1, X_2, X_3, X_4, X_5$
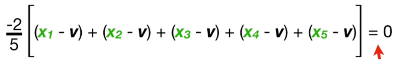
이것을 만족하는 v를 구한다.

n개의 표본을 뽑는다고 X_1, X_2, X_3, X_4, X_5,...,X_n 했을 때도 결과는 동일하다.

v는 n개의 표본의 평균에서 variance가 최소가 된다.
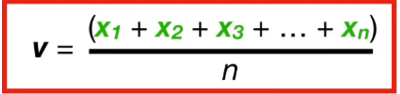
따라서 표본의 분산을 n으로 나누면 모분산 보다 항상 값이 작다.
표본평균이 모평균과 동일할 때가 아닌 이상 항상 작은데 그 두 값이 동일할 가능성은 전혀 없다.
따라서 표본의 분산을 n-1로 나누어서 모분산을 추정하는 것이다.
3) 표본분산을 구할 때 n이 아닌 n-1로 나누는 이유 (예)
$\overline{X}$의 위치를 옮겨가면서 분산을 구하고 그래프로 그려보자

$\overline{X}$의 값이 보라색 막대의 위치이다. x축은 보라색 막대의 위치이고 y축은 그 때의 분산값이다.
$\overline{X}$가 표본평균일 때 분산이 가장 작다.
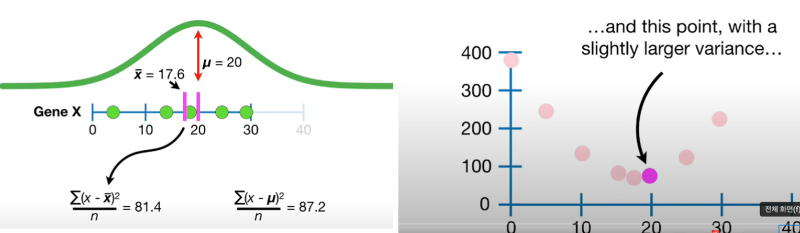
당연하게도 표본평균이 아닌 모평균의 값으로 분산을 구하면 이 값은 표본평균일때보다 크다.
따라서 우리가 만약 표본 평균을 사용한다면 모분산을 underestimate한 것이된다.
표본평균이 모평균보다 큰 경우에도 동일하다.
ref.
1. 통계학의 이해1, 여인권 교수님
2. statquest Why Dividing by N Underestimates the Variance

댓글