4. 인공신경망 (ANN, Artificial Neural Network) 개념
이번 시간에는 Artificial Neural Network (ANN)의 기본적인 개념에 대해서 알아볼게요
4. 인공신경망 (ANN, Artificial Neural Network) 개념
4-1. Neural network 구조
(1) 생명체의 Neural network
(2) Machine learning의 neural network
4-2. activation function
(1) 단위 계단 함수
(2) sigmoid function
4-3. McCulloch and Pitts (M-P) neuron
- weight와 threshold는 학습의 대상이다.
4-4. Multi-layer neural network
(1) multi-layer feedfoward neural networks (다층 순방향 신경망)
(2) 2-layer neural network
이전에 parameter의 종류, parameter tuning, cross validation, ROC curve 등 기계학습을 평가에 대해 전반적인 내용에 대해 알고싶다면 [딥러닝 독학] 3. 머신러닝 평가 방법
4-1. Neural network 구조
(1) 생명체의 Neural network
생명체의 neural network에서 각 neuron은 기타 neuron과 서로 연결되어 있다.
만약 neuron이 흥분한다면 연결된 neuron으로 화학물질을 전하여 neuron 내의 전압을 바꾼다.
이후 어떤 Neuron의 전압이 threshold를 넘으면 해당 neuron이 활성화된다.

(2) Machine learning의 neural network
1. Machine learning model에서 neuron은 n개의 기타 neuron에서 전송하는 입력 신호를 받는다.
→ 여기서 입력신호는 feature value이다.
2. feature value에 적절한 weight가 곱해진 형태로 최종 입력 신호를 받게 된다.
→ 이런 입력 신호는 weight (가중치)를 가진 connection (연결)을 거쳐 전달된다.
3. 받은 최종 입력신호들은 모두 합쳐지고 이 합쳐진 값은 threshold와 비교해서 처리된다.
→ neuron이 받은 총 입력값은 neuron의 threshold와 비교하고, activation function (활성화 점수)를 통해 neuron의 출력을 처리한다.
4. threshold와 비교한 후에 activation function으로 보정한다.
→ 그 다음 neuron으로 가는 입력신호는 feature value가 아니고 activation function에 의해 보정된 값이다.

neural network라고 하는 것은 잘 익은 수박과 잘 익지 않은 수박에 대해 feature value가 들어왔을 때 그 feature value가 activation function에 의해 변형되고 이 변형된 값을 통해 0과 1을 잘 나눌 수 있도록 연결되어 있는 신경망에서의 weight와 threshold를 학습하는 것을 최종 목표로 하고 있다.
4-2. activation function
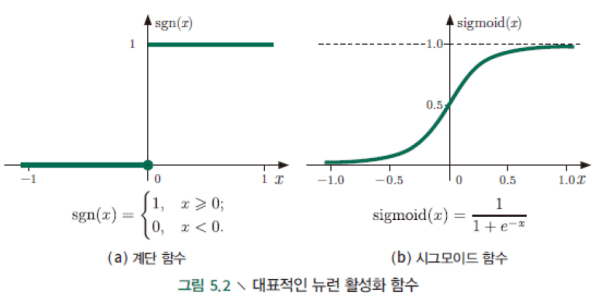
(1) 단위 계단 함수
가장 직관적인 activation function은 (a)에 보이는 단위계단함수이다.
이 함수는 입력값을 출력값 ‘0’이나 ‘1’에 투영한다.
신호전달의 형태는 보통 1과 0의 형태로 이루어진다.
→ 다음 neuron으로 신호를 전달한다 / 전달하지 않는다.
이전 신호들의 합이 0보다 작은 경우 전부 0으로 처리하고 그 값이 특정 threshold (여기서는 0)보다 큰 값을 가지고 있으면 전부 1로 처리한다.
‘1’은 neuron ‘흥분’에 해당하고 ‘0’은 neuron의 ‘억제’에 해당한다.
그러나 단위 계단 함수는 매끄럽지 못하고 불연속성이라는 좋지 않은 특성이 있다.
machine learning의 함수를 사용하기 위해서는 미분을 해야하는데 불연속성이 있는 함수를 사용하는 것은 부적합하다.
따라서 activation function으로는 sigmoid function을 자주 사용한다.
(2) sigmoid function
가장 대표적인 sigmoid function은 (b)이다.
그림에서 알 수 있는 것처럼 이 함수는 비교적 넓은 범위 내에서 변화하는 입력값을 (0,1) 사이의 출력값 범위 내로 밀어넣을 수 있다.
다양한 함수 중에 가장 연속적인 형태를 띠고 있으면서 신호의 전달의 형태를 잘 표현하는 함수 중의 하나가 sigmoid function이다.
$ y = f(\sum_{i =1}^{n}w_ix_i-\Theta )$
y = sigmoid function (전체 신호 값을 모두 합 - 임계값)
취합한 신호와 threshold의 차이를 구한 값을 함수에 x값으로 넣는다.
어떤 값이던 최종적으로는 0과 1사이에 위치하는 boundary가 정해지도록 activation function이 작동하게 된다.
이런 다수의 neuron을 일정한 겹층 구조로 연결하면 neural network를 얻게 된다.
4-3. McCulloch and Pitts (M-P) neuron

Neuron의 기본구조는 McCulloch and Pitts (M-P) neuron으로 불린다.
해당 neuron은 연결된 이전 neuron들의 입력값에 연결 weight의 총합을 받은 후, 임계값과의 비교 후 (threshold) activation function을 통하여 출력값을 생성한다.
이런 neuron을 M-P neuron이라고 부른다.
- weight와 threshold는 학습의 대상이다.
입력층 neuron들의 입력 신호 $(x_1, x_2,..)$에 각각에 고유한 weight $(w_1, w_2,..)$를 부여한다.
weight는 각 신호가 다음 연결 neuron에 주는 영향력을 조절하는 요소이다.
weight가 클수록 해당 신호가 그만큼 더 중요하다는 것을 의미한다.
w는 입력값이 출력값에 주는 영향력을 조절하는 parameter라면, threshold (실제 계산에서는 bias로 처리됨)는 neuron이 얼마나 쉽게 활성화 되느냐를 조절하는 parameter이다.
threshold 없이 그냥 weight를 곱한 값을 합쳐서 바로 activation function으로 넘어간다면 weight 이외에 우리가 조절할 수 있는 값이 없어지는 것이다.
하지만 합쳐진 neuron 안에서 조금 더 세밀하게 조절하기 위해서 threshold 값을 사용한다.
예를 들어, 선형회귀모델에서 y와 x와의 관계를 y = ax 만으로 표현한다면 a만을 가지고 이들의 관계를 설명하는 것이 불충분할 수 있다.
이 경우 b라고 하는 bias 개념을 넣어서 y = ax+b로 표현하는데 이것과 동일한 개념이다.
4-4. Multi-layer neural network
neuron의 아름다움은 “층을 쌓아” multi-layer neural network를 만들 수 있다는데 있다.
multi-layer feedfoward neural networks이 일반적으로 이야기하는 artificial neural network (ANN)의 가장 전형적인 형태이다.

위 그림에서 출력층과 입력층 사이에 한 층의 neuron이 있는데, 이를 hidden layer (은닉층)이라고 부른다.
hidden layer와 출력층 Neuron은 모두 activation function의 기능을 갖는다.
neural network 각 층의 neuron은 다음 층 Neuron과 완전 연결되어 있고, 같은 층의 neuron 끼리는 연결되지 않는다.
층을 뛰어넘는 연결도 존재하지 않는다.
(1) multi-layer feedfoward neural networks (다층 순방향 신경망)
위 그림과 같은 neural network 결합 구조를 일반적으로 multi-layer feedfoward neural networks (다층 순방향 신경망)이라고 부른다.
multi-layer로 되어있고 정보의 흐름이 한 방향으로 가는 neural network이다.
여기서 입력층 neuron은 외부 입력을 받고, hidden layer 와 출력층 neuron은 신호를 가공한다.
그리고 최종 결과는 출력층 Neuron에 의해 출력된다.
즉, 입력층 neuron에는 sample feature value만 들어가고 함수처리는 하지 않는다.
반면, hidden layer와 출력층은 기능성 Neuron을 포함한다.
(2) 2-layer neural network
위 그림은 또한 2층 neural network라고 불린다.
이런 구조는 hidden layer만 포함하면 되기 때문에 그냥 multi-layer neural network라고 간략히 부른다.
neural network 학습 과정에서는 training data를 통해 neuron 간의 connection weight (연결 가중치)와 각 가능성 neuron의 threshold만 조절하면 된다.
즉, Neural network가 학습하는 것은 모두 connection weight와 threshold에 내재되어 있다.
다음 시간에는 오차 역전파 알고리즘 (Backpropagation algorithm)에 대해 알아볼게요
ref.
edwith 기계학습 및 딥러닝 기초 이론과 암유전체 데이터 딥러닝 적용 실습 (2023)

댓글